Zadanie tygodnia #1 — ZQUERY

W tej serii wpisów proponuję ciekawe zadania wraz z opisem rozwiązań.

Treść zadania

Dana jest tablica $N$ liczb o wartościach ze zbioru $\{-1, 1\}$. Następnie dane jest $M$ zapytań składających się z dwóch liczb $l, r$. Dla danego zapytania należy odpowiedzieć, jaka jest długość najdłuższego przedziału zawierającego się w przedziale $[l, r]$ o sumie elementów równej $0$?

Zanim przejdziesz do przeczytania rozwiązania, spróbuj samemu pomyśleć nad rozwiązaniem, powiedzmy do godziny. Jeśli Ci się nie uda - wtedy wróć tutaj.

Zadanie można rozwiązać tutaj: https://www.spoj.com/problems/ZQUERY/.

Podpowiedzi

Zanim przejdziemy do pełnego rozwiązania, rozważmy kilka podpowiedzi.

Podpowiedź #1

Gdyby zapytania były postaci jaka jest suma elementów na przedziale $[l, r]$?, to z jakiej techniki można skorzystać?

Podpowiedź #2

Spróbuj się zastanowić, jak rozwiązać ten problem, gdyby dane było tylko jedno zapytanie.

Podpowiedź #3

Gdybyśmy umieli odpowiedzieć na zapytanie o przedział $[l, r]$, to czy jesteśmy w stanie odpowiedzieć na zapytanie o przedział $[l, r+1]$? A co z zapytaniem $[l + 1, r]$? Dlaczego z nim jest problem?

Pierwsze rozwiązanie

Pierwsza podpowiedź naprowadza nas na sumy prefiksowe $S$. Dzięki nim jesteśmy z łatwością w stanie stwierdzić, czy dany przedział $[l, r]$ ma sumę zero – jest tak tylko jedynie, gdy $S[l - 1] = S[r]$. Mamy zatem łatwy sposób, żeby w czasie stałym rozstrzygać, czy jakiś przedział ma odpowiednią długość.

Rozwiążmy teraz problem z drugiej podpowiedzi. Zauważ, że ta podpowiedź mogłaby równie dobrze być jednym z podzadań, gdyby było to zadanie z olimpiady.

Ustalmy $l$ oraz $r$. Przejdziemy pętlą od $l$ do $r$. Będziemy utrzymywać tablicę $left$, która dla danej sumy prefiksowej $s$ będzie utrzymywać pozycję skrajnie lewej pozycji $j \ge l$ takiej, że $S[j] = s$. Wtedy, dla każdej pozycji $i$, gdyby ona miała być prawym końcem naszego przedziału, jesteśmy w stanie znaleźć odpowiadający jej optymalny lewy koniec przedziału, jest w $left[S[i]] + 1$, a zatem długość tego przedziału to $i - left[S[i]] - 1$.

Rozwiązanie tej podpowiedzi daje nam od razu rozwiązanie pierwszej części kolejnej podpowiedzi. Widać również problem z przesunięciem lewego końca przedziału – jak zaktualizować tablicę $left$?

Po chwili przemyślenia okazuje się, że i ten problem da się rozwiązać – zamiast utrzymywać tablicę indeksów, możemy dla każdej sumy prefiksowej utrzymywać kolejkę dwustronną. Dzięki temu jesteśmy w stanie ‘‘wyrzucić’’ indeks $l$ z $left[S[j]]$ (analogicznie, gdybyśmy chcieli nasz przedział zawężać z prawej strony).

Prawdopodobnie widzisz już pełne rozwiązanie (ale jeśli nie, to się nie przejmuj!). Odpowiemy na zapytania offline (tj. niekoniecznie w kolejności, w której występują na wejściu). Do wyznaczenia kolejności, w jakich będziemy odpowiadać na zapytania, skorzystamy z algorytmu Mo.

Jeżeli nie znasz algorytmu Mo, koniecznie przeczytaj mój wpis Algorytm Mo opisujący ten algorytm!

W każdym momencie utrzymujemy aktywny przedział $[l, r]$. Kiedy odpowiemy na dane zapytanie, możemy przejść do następnego, przesuwając lewy i prawy koniec aktywnego przedziału do końców następnego zapytania. Musimy dodatkowo utrzymywać strukturę danych, na której będziemy utrzymywać aktualne długości przedziałów od sumie zerowej, np. multiset (nie da się utrzymywać tego w jednej zmiennej, ponieważ czasem musimy zwężać aktywny przedział). Z analizy algorytmu Mo wiemy, że całość będzie działać w czasie $\mathcal{O}(N\sqrt{M}\log{N} + M\log{N})$.

Niestety, ze względu na dodatkowy logarytm (którego nie da się łatwo pozbyć z tego rozwiązania – jeśli potrafisz, podziel się w komentarzu) nasze rozwiązanie prawdopodobnie dostanie TLE. Przedstawię teraz poprawę tego rozwiązania, które zupełnie pozbędzie się czynnika logarytmu.

Drugie rozwiązanie

Zauważmy, że dodatkowy logarytm wynika z konieczności utrzymywania struktury danych, do której łatwo możemy dodawać, jak i usuwać długości interesujących nas przedziałów. Gdybyśmy nigdy nie zwężali naszego przedziału, wtedy wystarczy jedna zmienna na utrzymywanie najdłuższego do tej pory znalezionego przedziału.

Przypomnijmy sobie działanie algorytmu Mo. Dzieli on zakres możliwych wartości końców zapytań na przedziały długości $K = N/\sqrt{M}$. W każdym kubełku rozważamy przedziały, których lewe końce zawierają się w tym kubełku, w kolejności rosnących prawych końców.

Podział interesujących przedziałów na trzy typy: 1. zupełnie poza kubełkiem, 2. zupełnie wewnątrz kubełka oraz 3. z lewym końcem w kubełku i prawym końcem poza kubełkiem

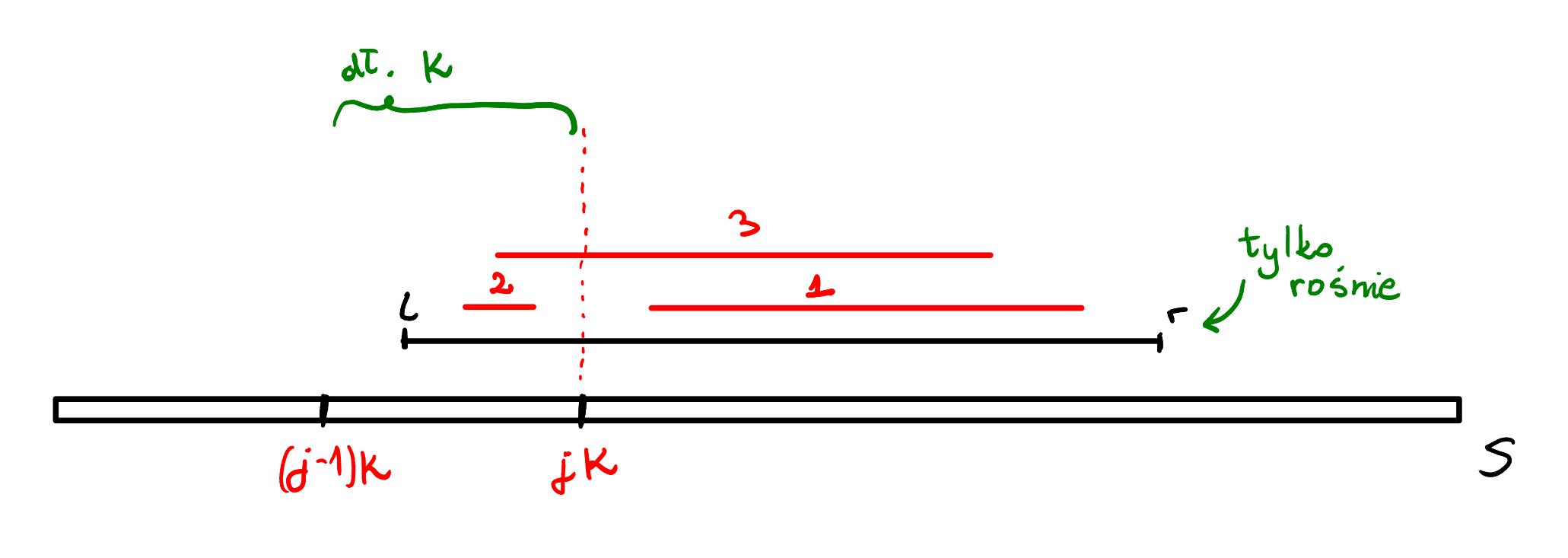
Spójrzmy na zapytanie z pewnego kubełka. Dla takiego przedziału $[l, r]$, poszukiwane podprzedziały mogą mieć jedną z trzech postaci: zawierać się zupełnie w kubełku, w ogóle nie zawierać się w kubełku, lub zaczynać się w kubełku i kończyć poza nim. Co to nam daje? Okazuje się, że jesteśmy w stanie obliczać maksymalną długość podprzedziałów o sumie zero każdego typu.

• Typ 1 Skoro $r$ tylko rośnie dla zapytań z lewym końcem wewnątrz tego samego kubełka, to możemy zastosować nasze rozwiązanie podpowiedzi drugiej dla wszystkich zapytań z tego kubełka!
• Typ 2 Skoro lewe końce mogą być od siebie oddalone dowolnie wewnątrz kubełka, to i tak musimy liczyć się z potencjalnym kosztem $K$ przy zmianie naszego aktywnego przedziału z jednego zapytania na kolejne. Dlaczego więc nie możemy więc brutalnie poszukać najlepszego podprzedziału tego typu dla każdego zapytania w czasie $\mathcal{O}(K)$?
• Typ 3 Podobnie jak z typem 2, możemy brutalnie sprawdzić każdy możliwy lewy koniec przedziału i dla niego znaleźć najlepszy prawy koniec poza kubełkiem. Aby to zrobić, wraz przesuwaniem prawego końca aktywnego przedziału utrzymujmy dodatkową tablicę $right[s]$, która dla danej sumy prefiksowej $s$ pamięta indeks skrajnie prawego elementu o sumie prefiksowej $s$.

Dla $j$-tego kubełka możemy przeprowadzić powyżej przedstawioną procedurę w czasie $\mathcal{O}(KM_j + N)$, gdzie $M_j$ oznacza liczbę zapytań w tym kubełku. Złożoność całego rozwiązania wynosi więc $\mathcal{O}(KM + N^2/K + M) = \mathcal{O}(N\sqrt{M} + M)$.

Szerszy kontekst

Powyższe rozwiązanie algorytmu Mo widziałem pod nazwą Mo and DSU, innymi słowy Mo + Union-find. Jest ogólnie użyteczne wszędzie tam, gdzie rozszerzenie przedziału jest proste, ale jego zwężenie nie do końca (tak jak w przypadku Union-find, w którym Union jest proste, ale możemy dokonywać rollbacków, o tym może w innym poście).