Algorytm Mo

We wpisie Zadanie tygodnia #1 opisałem ciekawe użycie algorytmu Mo. Przy okazji pisania wpisu zorientowałem się, że w polskim internecie trudno znaleźć materiały dotyczące tego algorytmu, a w języku angielskim nie znalazłem źródła, które pokazywałoby wizualny sposób zrozumienia tego algorytmu, który przedstawię poniżej. Jeżeli nie znasz algorytmu Mo, ten wpis jest dla Ciebie!

Zadanie

Dany jest ciąg liczb $a_1,\ldots, a_N$ o wartościach z przedziału $[-10^9, 10^9]$. Dane jest $Q$ przedziałów $[l, r]$, dla każdego z nich odpowiedzieć na pytanie – jaka jest najczęściej występująca liczba w tym przedziale?

Zadanie można rozwiązać na platformie solve.

Pierwsze podejście

W tego typu zadaniach warto zastanowić się, jak rozwiązalibyśmy problem, gdyby dane było tylko jedno zapytanie? W tym przypadku rozwiązań narzuca się kilka. Jednym z nich, na którym skupimy się w tym wpisie, jest utrzymanie tablicy liczącej liczbę wystąpień każdej z liczb, a następnie wybranie takiej, która występuje najczęściej. Ze względu na limity zadania, możemy użyć unordered_map<int, int> cnt lub przeskalować wartości po ich wczytaniu i korzystać ze zwykłej tablicy.

Poprawne, ale za wolne rozwiązanie

Powiedzmy, że policzyliśmy liczbę wystąpień każdej wartości na przedziale $[l, r]$. Zauważmy, że bardzo łatwo rozszerzyć naszą strukturę tak, żeby utrzymywała liczbę wystąpień wartości na przedziale $[l, r+1]$, $[l - 1, r]$, $[l+1, r]$ lub $[l, r - 1]$. Możemy zatem myśleć, że nasza tablica cnt utrzymuje stan na pewnym aktywnym przedziale $[l, r]$, który możemy dowolnie rozszerzać i zwężać z obu stron. Musimy również utrzymywać dodatkową strukturę danych, np. set<pair<int, int>> times, na której będziemy utrzymywać pary $\{ \text{liczba wystąpień } w, w\}$ i dzięki temu będziemy mieć łatwy dostęp do wartości występującą największą liczbę razy (times.rbegin()->second).

Ile zwężeń lub rozszerzeń należy wykonać, żeby aktywny przedział przemieścić z $[l_1, r_1]$ do $[l_2, r_2]$? Oczywiście $|l_1 - l_2| + |r_1 - r_2|$, a zatem koszt przejścia z jednego aktywnego przedziału do drugiego wynosi $\mathcal{O}((|l_1 - l_2| +|r_1 - r_2|)\log{N})$. To prowadzi nas do pełnego algorytmu:

1. Początkowo nasz aktywny przedział to $[1, 0]$ (tak, nie pomyliłem się, reprezentuje to pusty przedział).
2. Przechodzimy po każdym zapytaniu, przesuwając lewy i prawy koniec aktywnego przedziału do odpowiadających końców aktualnie rozpatrywanego zapytania.

Złożoność czasowa

Nietrudno zauważyć, że istnieją przykłady, dla których powyższy algorytm zadziała w czasie kwadratowym względem długości ciągu. Jeżeli zapytania zostaną nam podane przykładowo w takiej kolejności: $[1, 1], [1, N], [1, 1],\ldots$, przeniesienie aktywnego przedziału między kolejnymi zapytaniami zawsze będzie kosztować $N\log N$, co końcowo da złożoność $\mathcal{O}(QN\log N)$, zdecydowanie za dużą na limity zadania.

Wizualizacja algorytmu na płaszczyźnie

Narysujmy przykładowe trzy zapytania jako punkty na płaszczyźnie, pozioma oś oznacza lewe końce, a pionowa oś prawe końce przedziałów. Zauważmy, że daje to nową interpretację kosztu zmiany aktywnego przedziału – jest to odległość w metryce miejskiej między narysowanymi punktami (zwanej czasem metryką Manhattan).

Wizualizacja zmiany aktywnego przedziału między kolejnymi przedziałami. Przesunięcie lewego końca aktywnego przedziału to jak przejście równolegle do osi poziomej, a przesunięcie prawego równolegle do osi pionowej.

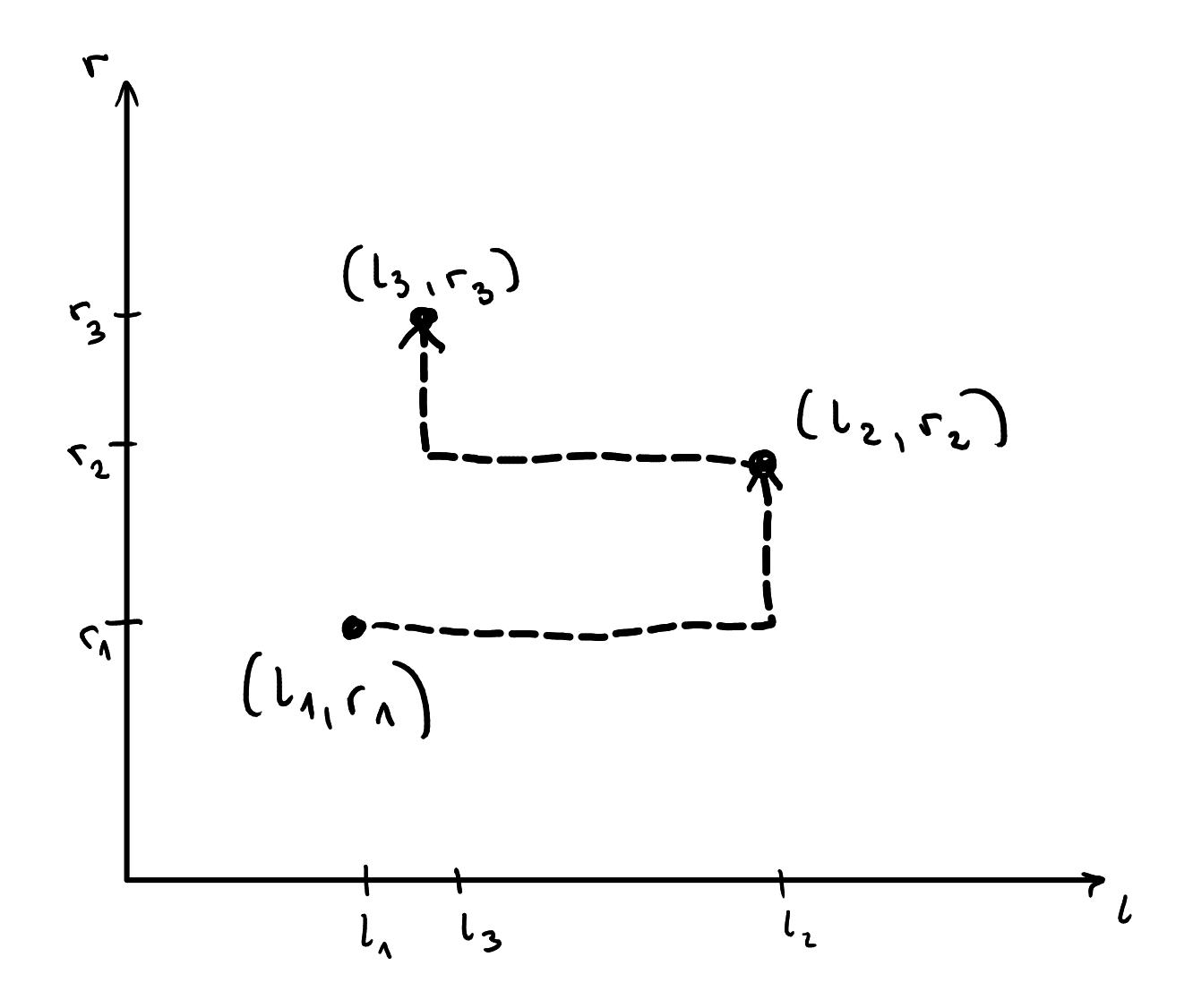
Zauważmy ponadto, że nikt nie zmusza nas do policzenia odpowiedzi w tej kolejności, w jakiej pojawiają się na wejściu. Możemy najpierw obliczyć odpowiedź dla każdego przedziału z wejścia w dowolnej kolejności, zapamiętać wyniki w tablicy, a dopiero potem wypisać wyniki na wyjście!

Przyspieszenie algorytmu

Dochodzimy do algorytmu Mo – zamiast obliczać odpowiedzi na zapytania w kolejności z wejścia, znajdźmy taką kolejność zapytań, która zminimalizuje sumaryczny koszt przejścia między zapytaniami, lub wedle naszej nowej interpretacji: zminimalizuje sumaryczną odległość na ścieżce przechodzącej po każdym wierzchołku na płaszczyźnie. Niestety, nie da się tego problemu szybko rozwiązać optymalnie (dla zainteresowanych, jest to podproblem problemu komiwojażera). Można zatem powiedzieć, że algorytm Mo jest algorytmem heurystycznym (w naszym wypadku poprawny, ale niekoniecznie optymalny).

Kluczowy koncept

Podzielmy nasze zapytania na kubełki długości $K$ (później okaże się ile powinno wynosić $K$). Posortujmy nasze zapytania tak, żeby:

1. Jeżeli lewe końce dwóch zapytań zapytań znajdują się w tym samym kubełku, to wcześniej rozpatrzmy zapytanie z mniejszym prawym końcem.
2. W przeciwnym wypadku najpierw rozważmy zapytanie, które zaczyna się wcześniej.

Ponownie, odwołując się do naszej graficznej interpretacji, łatwo można zilustrować jak będzie wyglądać ścieżka wyznaczona przez algorytm Mo.

Wizualizacja kolejności zmiany aktywnego przedziału wewnątrz kubełków.¹

Liczba przesunięć aktywnego przedziału

Policzmy zatem, jaki jest łączny koszt przechodzenia naszym aktywnym przedziałem między kolejnymi zapytaniami. Policzmy to z osobna dla każdego z $N/K$ kubełków i załóżmy, że w $i$-tym z nich rozpoczyna się $q_i$ przedziałów. Zatem w najgorszym razie, przechodząc między kolejnymi lewymi końcami zapytań z tego kubełka, musimy wykonać $q_iK$ przesunięć. Jednakże, prawe końce wewnątrz kubełka przesuwają się jedynie ‘‘w górę’’. Zatem za przesuwanie prawego końca nie zapłacimy więcej niż $N$ przesunięć.

Ponadto, dla każdego przejścia między kubełkami, musimy zapłacić potencjalne $2K + N$ przesunięć, ale robimy tak tylko $N/K$ razy. Sumując liczbę przesunięć aktywnego przedziału dla każdego kubełka i między nimi otrzymujemy łączną liczbę przesunięć $\mathcal{O}(QK + N^2/K + N)$. Licząc pochodną po $K$ otrzymujemy optymalną wartość $K = N/\sqrt{Q}$², a końcowa liczba przesunięć ograniczona jest przez $\mathcal{O}(N\sqrt{Q})$. Pamiętajmy jednak, że przesunięcie aktywnego przedziału w naszym przypadku kosztuje $\mathcal{O}(\log N)$ ze względu na set, który musimy utrzymywać, zatem końcowa złożoność całego algorytmu wynosi $\mathcal{O}(N\sqrt{Q}\log{N})$. Fajne, prawda?

Implementacja w C++

Jeśli myślisz, że implementacja tego algorytmu może być trudna, to nic bardziej mylnego! Poniżej przedstawiam łatwy sposób na wykorzystanie sort i szybkiego zdefiniowania komparatora, który będzie odpowiednio porównywał zapytania (tak, trzecim argumentem funkcji sort jest funkcja!). Z procedurą przesuwania aktywnego przedziału na pewno poradzisz sobie samodzielnie. W razie wątpliwości zostaw komentarz lub skontaktuj się ze mną bezpośrednio!

#define st first
#define nd second

/* {{l, r}, i} - lewy i prawy koniec oraz nr zapytania */
vector<pair<pair<int,int>, int> queries;

sort(queries.begin(), queries.end(), [](auto q1, auto q2) {
    if (q1.st.st / K != q2.st.st / K) {
        /* Zapytania mają lewe końce w różnych kubełkach. */
        return  q1.st.st < q2.st.st;
    }
    /* Zapytania w tym samym kubełku. */
    return q1.st.nd < q2.st.nd;
});

Ciekawostki

• Dodatkową optymalizacją tego algorytmu może być sortowanie parzystych kubełków w odwróconej kolejności prawych końców – dzięki temu nie musimy zmniejszać prawego końca o $N$, tylko potencjalnie o dużo mniej.
• Z tego algorytmu można korzystać również dla zapytań na poddrzewach oraz na ścieżkach w drzewie, ale o tym może w innym poście (dla zainteresowanych polecam ten blog na CF https://codeforces.com/blog/entry/43230).
• Wg tego posta na CodeForces, nazwa “algorytm Mo” wywodzi się od chińskiego zawodnika Mo Tao, który użył powyższego algorytmu do rozwiązania podobnego problemu.

Zadania

• MOcarna tablica (solve4)
• D-query (spoj)
• Zero query (spoj) (jak pozbyć się $\log{N}$ można przeczytać we wspominanym Zadaniu tygodnia #1)
• XOR and Favorite Number (CodeForces)
• Count on tree II (SPOJ), Mo na drzewie

1. Drobny szczegół, ale rysunek nie jest w pełni poprawny, ponieważ $r\ge l$ dla każdego zapytania, więc technicznie rzecz biorą punkty powinny znajdować się nad przekątną $x = y$. ↩

2. Możemy otrzymać tę wartość licząc pochodną po $K$ i szukając jej miejsca zerowego: $(QK + N^2/K)’ = Q - N^2/K^2 = 0$, z tego uzyskujemy już $K = N/\sqrt{Q}$. ↩