W tej serii wpisów proponuję ciekawe zadania wraz z opisem rozwiązań. Zachęcam do zajrzenia do poprzednich wpisów z tej serii. W tym tygodniu zajmiemy się zadaniem Kuglarz z Potyczek Algorytmicznych z 2014 roku. Jest to jedno z moich ulubionych zadań w ogóle, z bardzo eleganckim rozwiązaniem.

Treść zadania

Zadanie, wraz z treścią, można rozwiązywać tutaj. Również napiszę skrót treści.

Dane jest $N\le 2\,000$ kubków, pod każdym z nich może znajdować się kulka bądź też nie. Dla każdego przedziału kubków od $i$-tego do $j$-tego możemy dowiedzieć się, jaka jest parzystość liczby kulek w tych kubkach, musimy za to jednak zapłacić koszt $c_{ij}$. Jaki jest najmniejszy koszt, jaki musimy ponieść, żeby dla każdego kubka dowiedzieć się, czy znajduje się pod nim kulka?

Zanim przejdziesz do przeczytania rozwiązania, spróbuj samemu pomyśleć nad rozwiązaniem przez pewien czas. Jeśli Ci się nie uda - wtedy wróć tutaj.

Podpowiedzi

Zanim przejdziemy do pełnego rozwiązania, rozważmy kilka podpowiedzi.

Podpowiedź #1

Spróbuj znaleźć kilka ciągów przedziałów, które pozwoli jednoznacznie stwierdzić, jaka jest odpowiedź.

Podpowiedź #2

O ile minimalnie przedziałów musimy zapytać?

Podpowiedź #3

Załóżmy, że wybrałeś już kilka przedziałów, o które chcesz spytać. Dla jakich przedziałów możemy na tej podstawie wydedukować parzystość liczby kulek?

Rozwiązanie

Podpowiedź pierwsza ma wiele rozwiązań. Możemy przykładowo spytać o każdy przedział postaci $[i, i]$, dla $i$ od $1$ do $N$. Inną możliwością byłoby spytanie o każdy przedział $[1, 1], [1, 2], [1, 3],\ldots, [1,N]$. Można wymyślić jeszcze bardziej skomplikowane rozwiązania.

Niezależnie od tego, jaki ciąg przedziałów znaleźliśmy, można zauważyć, że ma on co najmniej $N$ przedziałów. Nie jest jeszcze jasne, czy nie da się lepiej, ale o tym przekonamy się rozważając następującą podpowiedź.

Załóżmy, że wybraliśmy dwa przedziały, które mają wspólny jeden z końców. Dzięki temu okazuje się, że dostaliśmy informacje o dodatkowym przedziale mimo tego, że nigdy o niego nie spytaliśmy. Przykładowo, jeżeli znamy parzystość liczby kulek na przedziałach $[1, 5]$ oraz $[6, 7]$, to w oczywisty sposób poznajemy również parzystość liczby kulek na przedziale $[1, 7]$. Dodatkowo, gdybyśmy poznali teraz parzystość przedziału $[4, 7]$, to moglibyśmy poznać również parzystość przedziału $[1, 3]$.

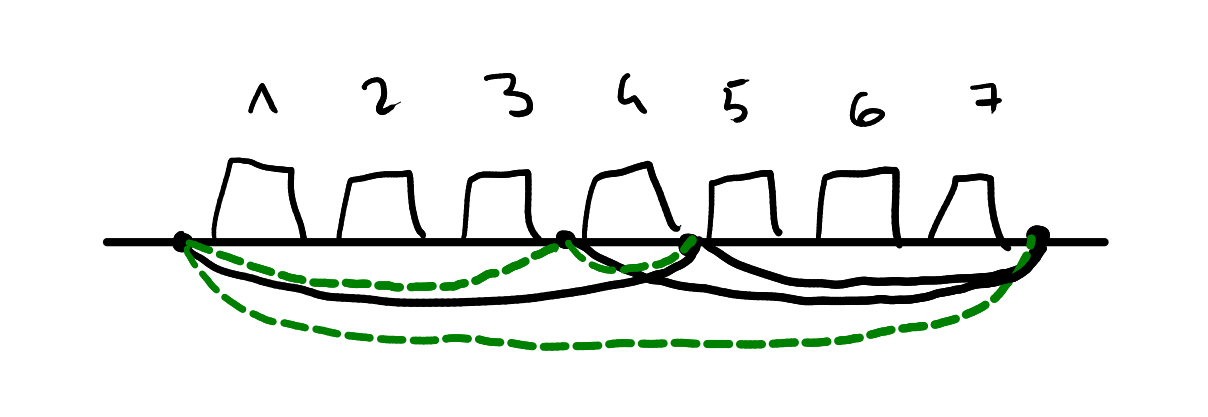
Z tych obserwacji nasuwa się następujący wniosek: jeżeli znamy parzystość liczby kulek na przedziałach $[l_1, l_2 - 1], [l_2, l_3 - 1],\ldots, [l_{k-1}, l_k]$, to możemy wydedukować parzystość liczby kulek na przedziale $[l_1, l_k]$. Co Wam to przypomina?

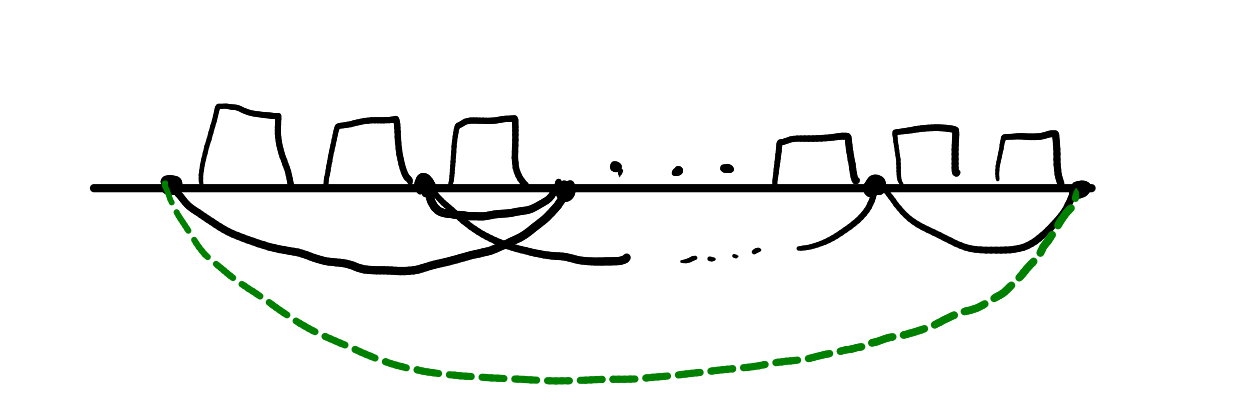
Możemy pomyśleć, że przedział kubeczków $[l, r]$ to tak naprawdę odcinek między wierzchołkami grafu o indeksach $l$ oraz $r+1$ o wadze $c_{lr}$. Zamiast przedziałów, pytamy teraz o krawędzie. Z naszej obserwacji wynika, że jeżeli wybierzemy krawędzie tak, że istnieje wśród nich ścieżka od pewnego wierzchołka $l$ do wierzchołka $r+1$, to znamy parzystość liczby kulek pod kubkami od $l$-tego do $r$-tego. Aby poznać, pod którymi kubkami jest kulka, musimy wybrać przedziały tak, żeby między każdymi wierzchołkami $l$ i $l+1$ istniała ścieżka. Rozwiązanie sprowadza się zatem do znalezienia minimalnego drzewa rozpinającego – łączymy ścieżkami wszystkie pary wierzchołków minimalnym możliwym kosztem. Zauważcie, że algorytm Kruskala kosztuje nas w tym wypadku $\mathcal{O}(N^2\log{N})$, a algorytm Prima możemy zaimplementować tak, żeby działał w czasie $\mathcal{O}(N^2)$, bez użycia kolejki priorytetowej.

Jeżeli nie wiesz, co to minimalne drzewo rozpinające, to nie przejmuj się. W polskim internecie jest sporo źródeł tłumaczących co to jest oraz dostępne są opisy algorytmów Kruskala i Prima. Moim zdaniem, niestety, żadne z nich nie tłumaczy porządnie tych algorytmów i trochę przekomplikowują sprawę. Możliwe, że sam napiszę o tym w przyszłości. Linki do wikipedii: